IDEF1X形式の実体−関連図
IDEF1X形式の概略
IDEF1X 形式の実体-関連図(ER図)は、大まかには以下のような決まりに従って書くことになっている。
- 実体型を長方形であらわし、実体型の名前を長方形の上に書く。
このとき使われる長方形には、角のある普通の長方形と角が丸くなっている長方形の2つがあり、ある基準に沿って使い分けることになっている。その基準については後述する。 - 実体型がもつ属性は、実体型をあらわしている長方形の中に、縦に属性の名前を列挙して並べて書く。
- 関連型を線であらわし、線の脇(上下左右の適当なところ)に関連型名を書く。 このとき使われる線には、実線と点線の2つがあり、ある基準に沿って使い分けることになっている。その基準については後述する。IDEF1X形式ではモデル設計の工夫をして関連型は属性を持たないようにしておく。
- 主キーとなっている属性を上から並べていき、主キー以外の属性との間に線を引き仕切る。主キーについては後に説明する。
- 関連型によって対応する実体の数をあらわすため、カーディナリティやオプショナリティと呼ばれるものに関する情報を記号や数、アルファベットで付け加える。カーディナリティやオプショナリティについては後に説明する。
例
「社員」が「部署」に「所属する」ことをあらわす IDEF1X形式の実体-関連図(ER図)を考えてみる。
実体型、関連型とそれぞれの持つ属性をここでは例えば、次のようなものとしてみる。
- 実体型
- 社員
属性:社員番号、入社年月日、所属部署 - 部署
属性:部署番号、部署名
- 社員
- 関連型
- 所属
このとき、実体-関連図は次のようになる。

この図では、主キーとそれ以外の属性を区切る線や、カーディナリティやオプショナリティをあらわすために記号 ● が付けられている。
主キー
主キーとは
実体-関連モデルでは、実体型が持つある1つの属性またはあるいくつかの属性を組にして考えたときに、その値により実体型に属している各実体を一意に識別でき、極小の組になっているものをその実体型の主キー(primary key)と呼ぶ。
ここで、極小であるというのは、その属性の組からどれか1つでも属性を取り除いてしまうとその実体型に属している各実体を一意に識別できなくなってしまうことが起きるような組であるという意味である。
主キーすることができる属性または属性の組は1通りとは限らず、複数考えられる場合がある。例えば、ある大学に在籍している「学生」という実体型を考えることにし、その属性として「学籍番号」、「氏名」、「学部」、「電話番号」を考えることにした場合、「学籍番号」という1つの属性のみでも個々の学生を一意に識別することができるし、「氏名」と「電話番号」という2つの属性を組にしたものでも個々の学生を一意に識別することができる。このような場合はデータ管理上最も適切であると考えられるものを主キーとすることが望ましいと言える。この実体型「学生」では「氏名」と「電話番号」を組にして「学生」を特定するより「学籍番号」を使って「学生」を特定するほうが大抵の場合望ましいと考えれれるので、「学籍番号」を主キーとする。
主キーのあらわし方
IDEF1X形式で実体-関連モデルをあらわす場合、実体型をあらわす長方形では、主キーとした属性または属性の組を上部に並べ、主キーとそれ以外の属性の間に線を引いて区切る。
例
実体型「学生」は属性「学籍番号」、「氏名」、「学部」、「電話番号」を持つとする。
次の図で、左の図は「学籍番号」を主キーとした場合で、右の図は「氏名」と「電話番号」を主キーとした場合である。
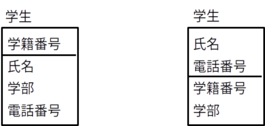
カーディナリティ(多重度)とオプショナリティ
カーディナリティ(多重度)
2つの実体型
つまり、
(もちろん
例
ある学校で、ある年度に、「教員」が「科目」を「担当する」という状況を考えてみる。
実体型として「教員」、「科目」を考え、その間の関連として「担当」を考えると次の図のようになる。ただし、この図では、まだ、カーディナリティやオプショナリティをあらわす記号は付けていない。
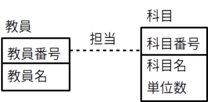
この学校では、各教員は1つ以上の科目を担当し、最大で3科目までを担当することができるとする。
- 実体「教員」から見たとき、関連「担当」で対応することがあり得る「科目」の個数の最大値は
- 実体「科目」から見たとき、関連「担当」で対応することがあり得る「教員」は必ず1人だけいるので、カーディナリティは
例
ある学校で、ある年度に、「教員」が「科目」を「担当する」という状況を考えてみる。つまり、実体型「教員」が関連型「担当」によって実体型「科目」と結びついているとする。
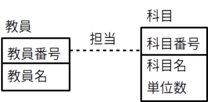
ここで次の2つの場合について考えてみる。
- この学校では、各教員は科目を1つまで担当できるとする。
この場合、実体型「教員」から見たとき、関連型「担当」で対応することがあり得る「科目」の個数の最大値は - この学校では、各教員は複数の科目を担当できるとする。
この場合、実体型「教員」から見たとき、関連型「担当」で対応することがあり得る「科目」の個数の最大値はない。つまり、実体型「教員」に属するそれぞれの教員にたいして、実体型「科目」に属する科目は多数(複数)存在することが許される。
オプショナリティ
2つの実体型
つまり、
(もちろん、
上記の 1. の場合「
例
ある学校で、ある年度に、「教員」が「科目」を「担当する」という状況を考えてみる。つまり、実体型「教員」が関連型「担当」によって実体型「科目」と結びついているとする。
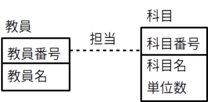
ここで次の2つの場合について考えてみる。
- この学校では、各教員は科目を少なくとも1つ担当しなければならないとする。
この場合、実体型「教員」から見たとき、関連型「担当」で対応することがあり得る「科目」の個数の最小値は - この学校では、各教員は科目を1つも担当しなくてもよいとする。
この場合、実体型「教員」から見たとき、関連型「担当」で対応することがあり得る「科目」の個数の最小値は
1対1・1対多・多対多の対応関係
2つの実体型
1対1
例
プロ野球の球団を監督が指揮をするという状況を考えてみる。つまり、実体型「球団」が関連型「指揮」によって実体型「監督」と結びついているとする。
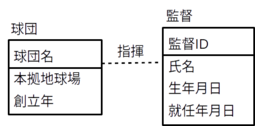
各球団にはただ1人監督が存在し、各監督は唯一つの球団を指揮する。つまり、実体型「球団」に属している各球団に対して、関連「指揮」によって実体型「監督」に属する実体が唯一つ対応し、実体型「監督」に属している各監督に対して、関連「指揮」によって実体型「球団」に属する実体が唯一つ対応する。よって、これは1対1の対応関係である。
1対多
例
ある国にある各飲料メーカーが商品を生産するという状況について考えてみる。つまり、実体型「飲料メーカー」が関連型「生産」によって実体型「商品」と結びついているとする。
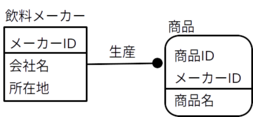
各飲料メーカーは普通、複数の種類の商品を生産し、それぞれの商品は1つの飲料メーカーによって生産される。つまり、実体型「飲料メーカー」に属しているメーカーに対して、関連「生産」によって実体型「商品」に属する実体が多数(複数)対応し、実体型「商品」に属している各商品に対して、関連「生産」によって実体型「飲料メーカー」に属する実体が唯一つ対応する。よって、これは1対多の対応関係である。
多対多
例
ある大学に在籍している各学生がその大学の授業で科目を受講するという状況を考えてみる。つまり、実体型「学生」が関連型「受講」によって実体型「科目」と結びついているとする。
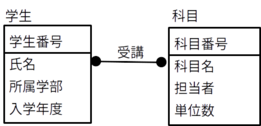
各学生は普通、複数の科目を受講し、それぞれの科目は普通、多数(複数)の学生によって受講される。つまり、実体型「学生」に属している学生に対して、関連「受講」によって実体型「科目」に属する実体が多数(複数)対応し、実体型「科目」に属している各科目に対して、関連「受講」によって実体型「学生」に属する実体が多数(複数)対応する。よって、これは多対多の対応関係である。
実体型の間の親子関係
2つの実体型
「
「
実体型の間の依存関係
親子関係にある実体型間の関連型は「依存」という観点から2つに分けて考えることができる。
実体型の依存関係と依存関連型
2つの実体型
例
ある会社が顧客から注文を受け、受注の情報を管理する場面を考えてみる。顧客が注文を行うと「受注日」、「顧客番号」の情報が受注側で管理され、さらに、一つひとつの注文はそこに含まれる注文された「商品」ごとに注文明細へと細分され、注文明細では注文された商品の「単価」、「数量」の情報が管理されるとする。また、顧客の情報として「住所」、「電話番号」を管理することにする。
このとき、
- 実体型
- 顧客
- 受注
- 受注明細
- 関連型
- 注文
- 細分
のように実体型と関連型を用意することができる。
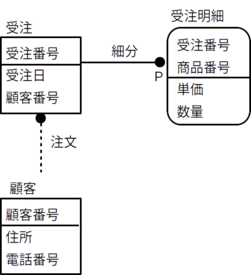
「受注」が存在しなければ、「受注明細」を考えることに意味はないので、「受注明細」は「受注」に従属している。(依存している。)
「受注」や「顧客」はどちらも、他の実体型が存在しなくても問題なく存在することができる。つまり、「受注」、「顧客」は自分以外のどの実体型からも独立している。(自分以外のどの実体型にも依存していない。)
先の例では、関連型「受注明細」は関連型「受注」に従属している。そして、「受注明細」の主キーは「受注番号」と「商品番号」であるが、これは「受注」の主キー「受注番号」を含んでいる。
先の例では、「細分」は依存関連型、「注文」は非依存関連である。
依存関係に応じた関連型のあらわしかた
IDEF1X形式では、依存関連型は実線であらわし、非依存関連型は点線であらわす。
先の例では、実体型「受注明細」は実体型「受注」に従属している。そして「受注明細」と「受注」は関連型「細分」で対応しているので「細分」は依存関連型である。そしてこの関連は実線であらわされる。
また、実体型「受注」と実体型「顧客」は関連型「注文」で対応しているが、「受注」は「顧客」に依存していないので「注文」は非依存関連である。そしてこの関連型は点線であらわされる。
注意
- 実体型の間に親子関係がある(つまり1対1または1対多となっている)からといって、子実体が親実体に依存しているとは限らない。
- 親子関係にない実体型の間の関連型(つまり多対多となっている)については依存関係を考えない。そして関連型は実線であらわすことになっている。
- 実体型の間に依存関係があるならば、必ず親子関係がある(つまり1対1または1対多となっている)。この場合、依存される方が親実体、依存する方が子実体である。
独立実体と従属実体
独立実体・従属実体とは
ある実体-関連図にあらわれているある実体型を
独立実体と従属実体のあらわしかた
IDEF1X形式では、独立実体は長方形の角はそのまま尖ったままにしてあらわし、従属実体は長方形の角を丸くしてあらわす。
例
例
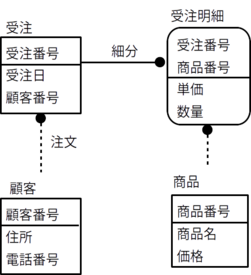
この図では、実体型「受注」は2つの実体型「受注明細」と「顧客」に関連しているがどちらにも依存していない。よって「受注」は独立実体(非依存実体)であり、長方形の角は尖ったままであらわす。
また、実体型「受注明細」は2つの実体型「受注」と「商品」に関連しているが、「受注」には依存している。よって「受注明細」は従属実体(依存実体)であり、長方形の角を丸くしてあらわす。
カーディナリティ(多重度)やオプショナリティをあらわす記号
IDEF1X形式の実体-関連モデルでは、関連型のカーディナリティやオプショナリティは以下に説明されるように、関連型をあらわす線(実線、点線)の両端に必要に応じて●や◇という記号、数、いくつかのアルファベットをつけてあらわすことになっている。
2つの実体型
IDEF1X形式では、親実体から子実体を見たときの多重度の表し方に主な関心が置かれている。実体間に親子関係があるのは、1対1または1対多の関連である。
IDEF1X形式では、親側であっても子側であっても、
また、実体間に依存関係がない場合、子実体から親実体を見たときに親側に対応する実体がないこともあり得るため、そのことをあらわす記号が用意されている。
1対1または1対多の場合
この場合、子実体から親実体を見たときの多重度は基本的に
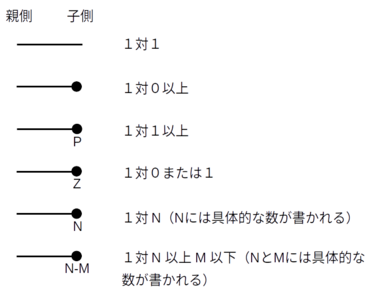
多対多の場合
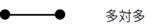
非依存関連型で親側に対応する実体がないこともあり得る場合
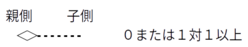
外部キー
2つの実体型
IDEF1X形式の実体-関連図では、ある実体型のある属性が外部キーであることを明示するために、実体型をあらわす長方形で縦に属性名を並べて書くとき、その属性名に「(FK)」を付け、「属性名(FK)」と書いておく。
例
次の図の実体型「受注」の属性「顧客番号」の値は実体型「顧客」の属性「顧客番号」に存在している値の中から必ず選ばれる。
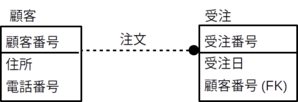
例
次の図の実体型「商品」の属性「メーカーID」の値は実体型「飲料メーカー」の属性「メーカーID」に存在している値の中から必ず選ばれる。

この例では、「商品」は「飲料メーカー」の子実体になっているのみならず、従属実体にもなっている(依存している)。そのため、外部キー「メーカー ID(FK)」は「商品 ID」とともに実体型「商品」の主キーを構成する。
IDEF1X形式ではあらわすことのできない関連型への対処
IDEF1X形式では関連型は線であらわされるだけなので属性を持つことができない。
この場合、親子関係のある実体型を結びつけている関連型(つまり1対1または1対多となっている)では、子実体の属性に親実体の主キーを付け加え、さらに、関連型の属性も付け加える。
多対多の関連型については後述する補足を参照のこと。
関連型は常に2つの実体型の間を線で結んであらわすため、3項関連型を取り扱うことはできない。
この場合、新しい実体型を導入して1対多の2項関係に書き換える。
補足
実体-概念図(ER図)はいずれ論理データモデル、例えばリレーショナルデータモデルへ変換されることになる。
多対多の関連型を IDEF1X形式であらわすことはできるが、リレーショナルデータモデルでは扱えない。そのため、多対多の対応がある場合、以下のどちらかの対応をする。
- 予め IDEF1X形式の実体-概念図(ER図)の段階で工夫する。この場合、新しい実体型を導入し多対多の対応を1対多の対応へ書き換えるようにする。
- リレーショナルデータモデルへ変換する際に工夫する。
後に説明するが、この場合、新しく、リレーション(リレーショナルで実体型に対応するもの)を導入し多対多の対応を1対多の対応に書き換えるようにする。
