リレーショナルデータモデルの作成
概念モデルの作成が終わったら、それを元に、コンピュータでの取り扱いに適した形にするために論理モデルを作成する。
論理モデルはこれまでに様々なものが考案されている。そして、現在最も多く使われている論理モデルはリレーショナルデータモデルと呼ばれているものである。
以下では、
- リレーショナルデータモデルとはどんなモデルなのか
- 実体-関係図(ER図)として作成された概念モデルをリレーショナルデータモデルへ変換する手法
について説明する。
リレーショナルデータモデル
リレーショナルデータモデルでは、データは表形式で取り扱われ、表はリレーション(relation)と呼ばれる。そして一般には、複数のリレーションがお互いに関連づけられてデータの管理、操作が行われることになる。
⚠ 実体-関連モデルで出てきた「関連型(relationship)」とリレーショナルデータモデルの「リレーション(relation)」は別の概念であることに注意。
リレーション
リレーショナルデータモデルで扱われるリレーション(つまり表)は、1行目に見出しがあり、2行目以降にデータが並べられているようなものである。例えば、次の例はある会社の顧客を取り扱うためのリレーション(つまり表)で、1行目の見出しには「顧客番号」、「顧客氏名」、「住所」、「電話番号」の項目が用意され、2行目以降には個別の顧客データが並べられている。
| 顧客番号 | 顧客氏名 | 住所 | 電話番号 |
|---|---|---|---|
| 0001 | 坂上裕一 | 東京都港区芝公園 ○-○-○ | 03-xxxx-xxxx |
| 0002 | 加藤美佳 | 埼玉県川口市青木 ○-○-○ | 048-xxx-xxxx |
| 0003 | 中村沙織 | 神奈川県平塚市浅間町 ○-○ | 0463-xx-xxxx |
繰り返しになるが、リレーショナルデータモデルではこのようなものを「表」と呼ぶのではなくリレーションと呼ぶ。
見出しに並べられている各項目は、実体-関連モデルにおける「属性」に対応している。また、2行目以降に並べられている個別のデータが、実体-関連モデルにおける「実体」に対応し、リレーションそのものが「実体型」に対応している。
属性
リレーションの1行目に並べられている各項目は属性と呼ばれる。また属性の個数はそのリレーションの次数と呼ばれる。
ドメイン
属性の値として取ることができる値の範囲をその属性のドメインと呼ぶ。
上にあらわれていたリレーション「顧客」の例では、
「顧客番号」という属性の値が取りうる範囲は「必要に応じてゼロ埋めされた4桁の正の整数の集合」
「顧客氏名」という属性の値が取りうる範囲は「任意の文字列の集合」
「住所」という属性の値が取りうる範囲は「任意の文字列の集合」または「住所表記として適切な文字列の集合」
「電話番号」という属性の値が取りうる範囲は「任意の文字列の集合」または「電話番号表記として適切な文字列の集合」
と考えることができる。
リレーションを数学の言葉で取り扱う
リレーションは、数学における集合の概念を使って定義することができ、リレーショナルデータモデルでのデータ操作も、集合の概念を使って理解することができる。
まず前置きとして、集合の直積について補足説明をしておく。
いくつかの集合 $X_1,X_2,\ldots,X_n$ があるとする。このとき、各 $X_1,X_2,\ldots,X_n$ から1つずつ要素 $x_1,x_2,\ldots,x_n$ を取り出し、それらを順番をそのままにし、かっこ ( ) を使って組にしたものを $(x_1,x_2,\ldots,x_n)$ と書くことにする。このようにして作ることができるありとあらゆる組全部の集合を $X_1,X_2,\ldots,X_n$ の直積と呼び、$X_1 \times X_2 \times \cdots \times X_n$ とあらわす。
つまり、数学の記法で説明すると、
$$
X_1 \times X_2 \times \cdots \times X_n
=\{(x_1,x_2,\ldots,x_n) \mid x_1 \in X_1,x_2 \in X_2,\ldots,x_n \in X_n \}
$$
である。
集合の直積という数学的な概念を使うと、リレーションは次のように考えることができる。
いま、いくつかの属性 $A_1,\ A_2,\ldots,\ A_n$ について考えているとする。そして、それらのドメインを $D_1,\ D_2,\ldots,\ D_n$ と書くことにする。このとき、これらドメインの直積 $D_1 \times D_2\cdots\times D_n$ の何らかの部分集合を考える。するとこれは属性 $A_1,\ A_2,\ldots,\ A_n$ をもつ何らかのリレーションを定義することになる。つまり、リレーションとは各属性のドメインの直積の部分集合のことであると理解することができる。
リレーションに属している要素はタプルと呼ばれる。
例
「社員」というリレーションがあり、「氏名」、「所属部署」という2つの属性を持っているとする。そして今、このリレーションは次の表のような、3人からなるものとする。
| 氏名 | 所属部署 |
|---|---|
| 田中一郎 | 営業部 |
| 島田由香里 | 開発部 |
| 遠山省吾 | 開発部 |
この場合、
属性「氏名」のドメインを $D_1$ とすると、$D_1$ は氏名として使うことが可能な文字を使ってできる文字列の集合と思うことができ、
属性「所属部署」のドメインを $D_2$ とすると、$D_2$ はこの会社に存在している部署名全てからなる集合と思うことができる。
そして、このリレーションに属しているタプルは
$$
\begin{align}
&(\text{田中一郎},\, \text{営業部}) \\[6pt]
&(\text{島田由香里},\, \text{開発部}) \\[6pt]
&(\text{遠山省吾},\, \text{開発部}) \\
\end{align}
$$
の3つとなる。また、このリレーション「社員」を集合の記号であらわすと、
$$
\{(\text{田中一郎}, \, \text{営業部}),\, (\text{島田由香里}, \, \text{開発部}),\,(\text{遠山省吾}, \, \text{開発部})\}
$$
となる。これは $D_1 \times D_2$ の部分集合になっている。
⚠ 現実の世界のデータを扱う場合、あるリレーションのある属性の値が定まっていないということがあり得る。例えば先の例のリレーション「社員」で、まだ配属先の部署が決定していない社員がいると、その社員の属性「所属部署」の値を決めることができない。このような場合、実用で使われるリレーショナルデータベースでは、空の値をもたせることができるようになっている。このような値は NULL値 や空値などと呼ばれる。
リレーショナルデータモデルにおけるタプルは、実体-関連モデルで実体型に属している個々の実体に対応するものと考えることができる。
スーパーキー・候補キー・主キー
あるリレーションにおいて、そのリレーションに属しているタプルを一意に識別できる属性または属性の組み合わせをスーパーキーという。
スーパーキーのうち、極小であるものを候補キーという。
候補キーのうち、業務を遂行するために最も適切であると考えられるものを主キーという。
外部キー
2つのリレーション $R_1$ と $R_2$ があり、$R_1$ のある属性 $A_1$ の値は、必ず、$R_2$ のある属性 $A_2$ に存在しているいる値の中から選ばれているようになっているとき、属性 $A_1$ は外部キー(foreign key)であるという。そしてこのとき、属性 $A_1$ は属性 $A_2$ を参照しているという。これは属性 $A_1$ に関してある種の制約がかかっていることを意味していて、特に参照整合性制約と呼ばれる。
リレーションスキーマ
リレーションは、表形式でデータを取り扱うもので、表の1行目に見出しとして様々な項目(属性と呼ばれる)が並べられ、2行目以降にデータが並べられる。また、各属性は、属性値として取ることができる値の範囲(つまり、その属性のドメイン)を持ち、さらに各属性にたいして何かしらの制約が課されていることもある。このような意味で、リレーションの持つデータは、構造を持っていることになる。
リレーションのデータが持つ構造をリレーションスキーマと呼ぶ。
あるリレーションが持つデータの構造(つまりリレーションスキーマ)をあらわすために、リレーション名、属性名を列挙して書くということが良く行われる。
例
| 顧客番号 | 顧客氏名 | 住所 | 電話番号 |
|---|---|---|---|
| 0001 | 坂上裕一 | 東京都港区芝公園 ○-○-○ | 03-xxxx-xxxx |
| 0002 | 加藤美佳 | 埼玉県川口市青木 ○-○-○ | 048-xxx-xxxx |
| 0003 | 中村沙織 | 神奈川県平塚市浅間町 ○-○ | 0463-xx-xxxx |
このリレーションのデータ構造は、
顧客(顧客番号, 顧客氏名, 住所, 電話番号)
のようにあらわされる。
この例で示されように、リレーション名をまず書き、それに続けてかっこの中に属性をカンマで区切って列挙して書けばよい。
この例で、各属性のドメインも明示したい場合は、
$$
\text{顧客}(\text{顧客番号}:D_1,\ \text{顧客氏名}:D_2,\ \text{住所}:D_3,\ \text{電話番号}:D_4)
$$
のように書く。ただしここで、$D_1$ は属性「顧客」のドメイン、$D_2$ は属性「顧客氏名」のドメイン、$D_1$ は属性「住所」のドメイン、$D_1$ は属性「電話番号」のドメインである。
またさらに、主キーとなっている属性には下に実線を引き、外部キーとなる属性があれば下に破線を引くということが行われる。例えば先の例では顧客番号を主キーとすることができるので、
顧客(顧客番号, 顧客氏名, 住所, 電話番号)
のように書くことができる。
概念モデルから論理モデルへ
実体-関連モデルからリレーショナルデータモデルへ
実体-関係図(ER図)として作成された概念モデルをリレーショナルデータモデルへ変換する手法を説明する。
概念データモデルの1つである実体-関連モデルでは、モデル化対象の世界は実体と関連であらわされ、実体や関連は属性と呼ばれるものを持つことができた。また、実体-関連モデルを図であらわす方法(つまり、実体-関係図(ER図))がいくつも考案されていて、代表的なものとして、ピーター・チェン記法、バックマン線図、IE形式、IDEF1X形式などがあるのだった。
論理データモデルの1つであるリレーショナルデータモデルでは、データは表形式で取り扱われ、表はリレーションと呼ばれた。また、リレーションは属性を持つことができた。
このようなことを思い出せば想像できるように、実体-関係図(ER図)として作成された概念モデルをリレーショナルデータモデルへ変換するためには、実体型や関連型をリレーションに変換する必要がある。そしてそれは、必要に応じて多少の工夫をしながら自然な方法で行われる。
以下、IDEF1X形式の実体-関係図(ER図)からリレーショナルデータモデルを作成する手法を概観する。
実体型からリレーションへの変換
実体型の名前をそのままリレーション名とし、実体型が持っている属性をそのままリレーションの属性とすれば良い。
例
実体型「学生」をリレーションへ変換
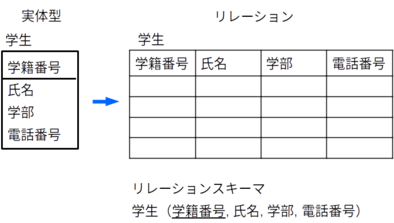
補足:「依存」という観点から、実体型は2つの種類に分けて考えることができた。従属実体(他の何らかの実体型が存在していないと意味がない実体)と、独立実体(他のどの実体型が存在していなくても自ら存在することができる実体)である。
ピーター・チェン記法では独立実体型に対応するものは通常実体型(または強実体型)と呼ばれ、従属実体型に対応するものは弱実体型と呼ばれている。この記法では、IDEF1X 形式で書かれた ER 図とは違い、弱実体型は、それに属している各実体を一意に識別できる属性または属性の組を持たず、それが従属している通常実体型(このとき、それはその弱実体型の親となっている)の主キーと組にすることにより、初めてそれぞれの実体を一意に識別できるようになる属性(これは部分キーと呼ばれている)を持っている。
このような事情から、ピーター・チェン記法で作成された ER 図から弱実体型をリレーションへ変換する場合、その弱実体型の属性だけではなくそれが従属している通常実体型の主キーとなっている属性も加えてリレーションを作ることになる。そして通常実体型から新たに加えられた主キーと、弱実体型がもともと持っていた部分キーを組み合わせたものがその弱実体型から作られるリレーションの主キーとなる。
関連型からリレーションへの変換
すでに説明したように、IDEF1X 形式では関連型は線であらわされるだけなので属性を持つことができない。また、関連型は常に2つの実体型の間を線で結んであらわすため3項関連型を取り扱うことはできない。そして、このような問題をクリアするために、(リレーショナルデータモデルへ変換する前に)IDEF1X 形式の実体-関連モデルの段階で、新しい実体型を導入して1対多の2項関係に書き換えるということが行われるのであった。そのため、新しく導入される実体型をリレーションに変換すればよい(関連型をリレーションに変換する必要はない)。
一方、多対多の関連型については以下のようにして新たにリレーションへ変換する。
まず、この、多対多の関連型で結び付けられているそれぞれの実体型からそれぞれの主キーを選びリレーションの属性とする。そして、このようにして選んだ主キーの組がリレーションの主キーとなる。
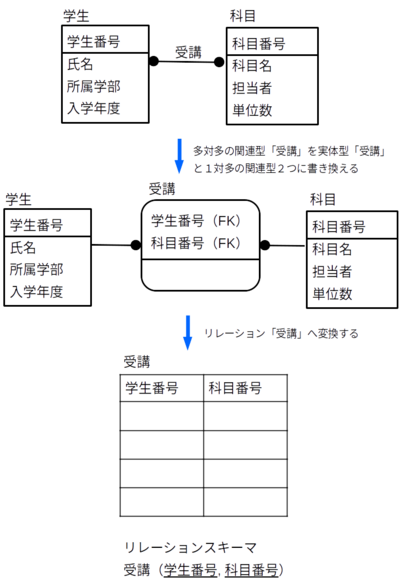
例
次の図では、多対多の関連型「受講」をまず、新たな実体型「受講」を導入し、1対多の関連型2つによって結びつけ、その後でリレーションへ変換している。この仕組みに納得がいっているなら、関連型「受講」をいきなりリレーション「受講」へ変換して良い。